GI1 - fractions rationnelles

Construction algébrique

Soit K un corps commutatif (en général $mathbb C$ ou $R$ ). On démontre que l'ensemble des polynômes à une indéterminée, à coefficients dans K est un anneau commutatif unitaire intègre noté K[X] . On peut alors construire son corps des fractions, noté K(X) : Sur l'ensemble des couples éléments de K[X] ×K[X]*, on définit

Une relation d'équivalence ~ par :(P,Q) ~ (P', Q') si et seulement si PQ' = QP'
Une addition : (P,Q) + (P',Q') = (PQ' + QP', QQ')
Une multiplication : (P,Q)(P', Q') = (PP',QQ')

L'ensemble des classes d'équivalence muni de l'addition et du produit induit est alors un corps commutatif appelé corps des fractions rationnelles. Tout couple (P, Q) où Q n'est pas le polynôme nul, est alors un représentant d'une fraction rationnelle. L'application qui à tout polynôme P, associe la classe de (P, 1) est un morphisme d'anneau injectif qui plonge K[X] dans K(X).

article détaillé : corps des fractions

Fraction irréductible : un couple (P, Q) tel que P et Q soient premiers entre eux ^[1] est appelé un représentant irréductible de la classe de (P, Q) et tout autre représentant (P', Q') de la même classe est tel qu'il existe un scalaire λ tel que P' = λP et Q' = λQ. Il existe plusieurs représentants irréductible d'une même classe mais un seul représentant irréductible dans lequel Q est un polynôme unitaire ^[2]: c'est la fraction irréductible unitaire représentant la classe.

Degré d'une fraction : Pour toute fraction rationnelle F, l'élément de $mathbb Z cup {- infty}$ défini par deg(P) - deg(Q) (où (P, Q) est un représentant de F) est indépendant du représentant de F et est appelé degré de F. Le degré d'une fraction vérifie les propriétés suivantes :

pour toutes fractions F et F' , deg(F + F') ≤ sup(deg(F), deg(F'))

pour toutes fractions F et F', deg(FF') = deg(F) + deg(F')

Racine et pôle : Si (P, Q) est la fraction irréductible représentant F, est racine de F toute racine ^[3] de P, est pôle de F toute racine de Q.

Cas des fractions rationnelles sur l'ensemble des réels

On peut munir le corps $mathbb{R}(mathrm{X})$ de la relation d'ordre définie par $mathrm{F} leq mathrm{G}$ si on a $mathrm{F}(t) leq mathrm{G}(t)$ pour réel t assez grand. Cette relation est alors totale. De plus, elle est compatible avec l'addition et la multiplication par les éléments positifs: $mathbb{R}(mathrm{X})$ a ainsi une structure de corps ordonné, et contient un sous-corps isomorphe à $mathbb{R}$ . Il n'est pas archimédien : en effet, on a $0 < frac{1}{mathrm{X}} < 1$ mais, pour tout entier naturel n, $n cdot frac{1}{mathrm{X}} < 1$ .

D'une manière générale, en posant |F| = max(-F, F), on dira que F est infiniment petit devant G (noté F ≪ G) si, pour tout entier naturel n, n⋅|F| < |G|.

Le degré fournit alors une échelle d'infiniment petits et d'infiniment grands par rapport aux réels : F ≪ G si, et seulement si, deg(F) < deg(G).

L'ensemble des éléments de $mathbb{R}(mathrm{X})$ devant lesquels les réels non nuls ne sont pas négligeables, i.e. ceux de degré inférieur ou égal à 0, forment un sous-anneau de $mathbb{R}(mathrm{X})$ .

Quelles différences entre fraction rationnelle et fonction rationnelle ?

À toute fraction rationnelle F, de représentant irréductible (P, Q), on peut associer une fonction rationnelle ƒ définie pour tout x tel que Q(x ) est non nul, par $f(x) = frac{mathrm{P}(x)}{mathrm{Q}(x)}$ . Cette association comporte cependant quelques risques :

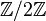
d'une part, il se peut, si le corps K est fini, que la fonction ƒ ne soit jamais définie : prendre par exemple $mathrm{F} = frac{1}{mathrm{X}^2 + mathrm{X}}$ sur le corps $mathbb Z/2mathbb Z$
d'autre part, la somme ou le produit de deux fractions ne peut s'effectuer que sur l'intersection des ensembles de définition et ne permet pas de transmettre les propriétés de corps : prendre par exemple F = X et $mathrm{G} = frac{1}{mathrm{X}}$ alors ƒ(x ) = x , $g(x) =frac 1x$ , $fg(x) = frac xx = 1$ seulement sur $R^*$

On peut toutefois, dans les cas de corps comme $mathbb C$ ou $R$ , construire un isomorphisme entre l'ensemble des fractions rationnelles et l'ensemble des fonctions rationnelles modulo la relation d'équivalence suivante :

ƒ ~ g si et seulement s'il existe un réel A tel que , pour tout x tel que |x | ≥ A, ƒ(x ) = g (x )

Cela revient à choisir le plus grand prolongement par continuité d'une fonction rationnelle.

Fraction rationnelle à plusieurs variables

Si K est un corps, l'ensemble des polynômes en plusieurs indéterminées K[X_1, X_2, ...X_n] reste un anneau commutatif unitaire intègre dont on peut chercher aussi le corps des fractions appelé corps des fractions rationnelles K(X_1, X_2, ..., X_n)

EXERCICES

Décomposer en éléments simples la fraction rationnelle définie sur $mathbb{R}setminus {-1, -2, -3}$ par

$F(x) = frac{2}{(x+1)(x+2)(x+3)}$

EXO 2

Soit 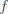$f$ la fonction définie par : $f(x) = frac{2x^2}{x^2 - 1} - frac{3}{x^2 + x - 2}$ .
1. Déterminer l'ensemble de définition de 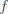$f$ .
2. Factoriser chacun des polynômes $x^2 - 1 text{ et } x^2 + x - 2$ .
3. a) Déterminer un dénominateur commun aux fractions rationnelles $frac{2x^2}{x^2 - 1}$ et $frac{3}{x^2 + x - 2}$ puis écrire $f(x)$ à l'aide d'une fraction rationnelle, notée $frac{g(x)}{h(x)}$ .
b) Déterminer une racine simple du polynôme g(x).
c) Simplifier l'écriture de $f(x)$ et résoudre l'équation $f(x) = 0$ .