GI1 - Les matrices

Définitions

Une matrice à m lignes et n colonnes est un tableau rectangulaire de mn nombres, rangés ligne par ligne. Il y a m lignes, et dans chaque ligne n nombres.

Passons maintenant à la définition formelle. Soient $A$ un ensemble et (m,n) un couple d'entiers positifs. Le plus souvent, l'ensemble $A$ est muni d'une structure de corps commutatif mais on utilise aussi fréquemment des matrices à coefficients dans un anneau.

On appelle matrice à coefficients dans A, de dimension (ou taille) (m,n) (c'est-à-dire à m lignes et n colonnes), une famille (a_i,j) d'éléments de A indexée par le produit cartésien des ensembles de nombres entiers $[1, m]$ et $[1, n]$ .

La matrice M pourra être notée par

$M=(a_{i,j})_{1le ile m,1le jle n}$

ou plus simplement (a_i,j) si le contexte s'y prête.

On représente généralement une matrice sous la forme d'un tableau rectangulaire. Par exemple, est représentée ci-dessous une matrice M, à coefficients entiers, et de dimension (3,4) :

$M=begin{pmatrix} 0 &1 & 2 & 3 4 & 5 & 6 & 7 8 & 9 & 10 & 11 end{pmatrix}$

Dans cette représentation, le premier coefficient de la dimension est le nombre de lignes, et le deuxième, le nombre de colonnes du tableau. Une matrice pour laquelle le nombre m de lignes est égal au nombre n de colonnes sera dite matrice carrée de taille n. Une matrice ne comportant qu'une seule ligne et n colonnes est appelée matrice ligne de taille n. Une matrice ne comportant m lignes et une seule colonne est appelée matrice colonne de taille m.

Pour repérer un coefficient d'une matrice, on indique son indice de ligne puis son indice de colonne, les lignes se comptant du haut vers le bas et les colonnes de la gauche vers la droite. Par exemple, on notera a_i,j, les coefficients de la matrice M, pour 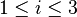$1le ile 3$ désignant le numéro de la ligne sur laquelle figure le coefficient envisagé, et $1le jle 4$ désignant son numéro de colonne ; ainsi a_2,4=7.

La disposition générale des coefficients d'une matrice M de taille (m,n) est donc la suivante

$M=begin{pmatrix} a_{1,1} & a_{1,2} & cdots & a_{1,n} a_{2,1} & a_{2,2} & cdots & a_{2,n} vdots & vdots & ddots & vdots a_{m,1} & a_{m,2} & cdots & a_{m,n} end{pmatrix}$

Pour effectuer certaines opérations, il peut être utile de travailler sur le système des lignes ou des colonnes d'une matrice. On pourra alors l'écrire sous une des formes suivantes

$M=begin{pmatrix} L_1L_2vdots L_mend{pmatrix}$ ou $M = begin{pmatrix} C_1 & C_2 & dots & C_n end{pmatrix}$ .

L'ensemble des matrices à coefficients dans A possédant m lignes et n colonnes est noté $M m, n (A)$ (ou parfois $M (m, n, A)$ ).

Lorsque m=n on note plus simplement $M n (A)$ .

Soit $M= (a_{i,j})_{1le ile m, 1le jle n} in M_{m,n}(A)$ , on appelle transposée de $M$ la matrice $^tM=(a_{j,i})_{1le jle n, 1le ile m}$ . Remarquons que $^tMin M_{n,m}(A)$ .

Par exemple, avec la matrice M des exemples précédents, on a

$^tM=begin{pmatrix} 0 & 4 & 8 1 & 5 & 9 2 & 6 & 10 3 & 7 & 11 end{pmatrix}$

L'opération de transposition est involutive, c'est-à-dire que $^t{}(^t!M)=M$ .

Espaces de matrices

On suppose maintenant que A est muni d'une structure d'anneau unitaire ; les éléments de A seront appelés scalaires, par opposition aux matrices dont nous allons voir qu'elles peuvent être considérées comme des vecteurs.

Addition et multiplication par un scalaire [modifier]

On définit sur $M m, n (A)$ une loi de composition interne provenant de l'addition des scalaires :

(a i, j) + (b i, j) = (c i, j)

ou $displaystyle c_{i,j}=a_{i,j}+b_{i,j}$

On ne peut additionner que deux matrices de même taille.

Exemple :

$begin{array}{l} begin{pmatrix} 0 &1 & 2 & 3 4 & 5 & 6 & 7 end{pmatrix} + begin{pmatrix} 0 &0 & 1 & 1 0 & 1 & 0 & 1 end{pmatrix} = begin{pmatrix} 0 &1 & 3 & 4 4 & 6 & 6 & 8 end{pmatrix} end{array}$

Pour chaque valeur du couple (m,n), l'espace $M m, n (A)$ devient alors un groupe abélien, d'élément neutre la matrice nulle, celle dont tous les coefficients valent 0.

On définit aussi une opération à gauche de A sur chaque espace $M m, n (A)$ en associant à chaque matrice $(a i, j)$ à coefficients dans A et chaque scalaire $λ$ dans A, la matrice $λ(a i, j) = (λ a i, j)$ obtenue en effectuant la multiplication, dans A, de tous les coefficients de la matrice initiale par $λ$ : c'est la multiplication par un scalaire.

En reprenant toujours la matrice M du premier exemple :

$2M=begin{pmatrix} 0 &2 & 4 & 6 8 & 10 & 12 & 14 16 & 18 & 20 & 22 end{pmatrix}$

Les espaces $M m, n (A)$ ainsi obtenus ont donc une structure de A-module à gauche, et plus particulièrement de A-espace vectoriel, si A est un corps commutatif.

Base canonique de l'espace des matrices

Alors $M m, n (A)$ est un $A$ -module libre de dimension $m n$ , muni d'une base canonique $(E_{i,j})_{1le ile m, 1le jle n}$ . La matrice $E i, j$ est celle dont tous les coefficients sont nuls sauf celui d'indice $(i, j)$ , qui vaut 1.

Pour toute matrice M, les coordonnées dans la base canonique sont les coefficients

$M = sum _{1le ile n, 1le jle p} a_{i,j} E_{i,j}$

Exemple :

$begin{pmatrix} 0 &1 & 2 4 & 3 & 1 end{pmatrix} = 0cdot begin{pmatrix} 1 &0 & 0 0 & 0 & 0 end{pmatrix} + 1cdot begin{pmatrix} 0 &1 & 0 0 & 0 & 0 end{pmatrix} + 2cdot begin{pmatrix} 0 &0 & 1 0 & 0 & 0 end{pmatrix} + 4cdot begin{pmatrix} 0 &0 & 0 1 & 0 & 0 end{pmatrix} + 3cdot begin{pmatrix} 0 &0 & 0 0 & 1 & 0 end{pmatrix} + 1cdot begin{pmatrix} 0 &0 & 0 0 & 0 & 1 end{pmatrix}$

Produit matriciel

Article détaillé : Produit matriciel.

On commence par définir le produit d'une matrice ligne par une matrice colonne. Soit n un nombre entier, L une matrice ligne, x_i ses coefficients, C une matrice colonne, y_i ses coefficients. On les suppose toutes deux de taille n. On définit alors le produit, considéré comme un scalaire ou une matrice de dimension (1,1) :

$LC = begin{pmatrix}x_1&dots&x_nend{pmatrix}begin{pmatrix}y_1vdots y_nend{pmatrix}=sum_{1le ile n} x_iy_i$

On remarque la condition de compatibilité sur les tailles des matrices (égalité du nombre de colonnes de la première avec le nombre de lignes de la deuxième). On définit maintenant plus généralement un produit entre deux matrices, la première, (x_i,j) dans $M m, n (A)$ , la deuxième, (y_i,j) dans $M n, p (A)$ , toujours avec une condition de compatibilité sur les tailles (et l'ordre des facteurs de la multiplication ne peut en général pas être changé). Le résultat obtenu est une matrice de $M m, p (A)$ , dont les coefficients (z_i,j) sont obtenus par :

$z_{i,j}=sum_{1le k le n} x_{i,k}y_{k,j}=x_{i,1}y_{1,j}+x_{i,2}y_{2,j}+cdots+ x_{i,p}y_{p,j}$

À la lumière de l'exemple de la multiplication d'une matrice ligne par une matrice colonne, on peut reformuler cette définition en disant que ce coefficient est égal au produit de la ligne i de la première matrice par la colonne j de la deuxième, ce qui s'écrit de la manière suivante, si les L_i sont les lignes de la première matrice, et les C_j les colonnes de la deuxième, le produit est : $begin{pmatrix}L_1vdots L_mend{pmatrix}begin{pmatrix}C_1&dots&C_pend{pmatrix}=begin{pmatrix} L_1C_1 & L_1C_2 & dots & L_1C_pL_2C_1 & L_2C_2 & dots & L_2C_p vdots & vdots & & vdots L_mC_1 & L_mC_2 & dots & L_mC_pend{pmatrix}$ .

Pour calculer en pratique un produit, il est nécessaire de visualiser l'opération. On considère le coefficient $c 1,2$ de la matrice produit MN si M est une matrice de type (4, 2), et N est une matrice de type (2, 3).

$c_{1,2} = sum_{r=1}^2 a_{1,r}b_{r,2} = a_{1,1}b_{1,2}+a_{1,2}b_{2,2}$

Le produit matriciel est associatif, distributif à droite et à gauche par rapport à l'addition matricielle. En revanche, même si les dimensions permettent de donner un sens à la question, même si l'anneau des scalaires est commutatif, un produit de matrices ne commute en général pas : MN n'est pas égal à NM, par exemple :

$M =begin{pmatrix} 0 & 0 1 & 0 end{pmatrix} quad N =begin{pmatrix} 1 & 0 0 & 0 end{pmatrix} quad MN =begin{pmatrix} 0 & 0 1 & 0 end{pmatrix} quad NM =begin{pmatrix} 0 & 0 0 & 0 end{pmatrix}$

Remarque : le produit de deux matrices non nulles est peut être nul, comme l'exemple au-dessus.

Ce contre-exemple prouve même que les matrices MN et NM ne sont pas toujours semblables.

Lorsque l'anneau des scalaires est commutatif, la transposition et le produit matriciel vérifient la propriété :

$forall Min M_{n,p}(A), forall Nin M_{p,q}(A), ^t(MN)=^tN,^t!M$

Matrice identité et inverse d'une matrice

Pour chque nombre entier n, on note I_n la matrice carrée de taille n dont les coefficients diagonaux sont égaux à 1 et dont les autres coefficients sont nuls ; elle est appelée matrice identité de taille n.

$I_1=1quad I_2= begin{pmatrix} 1 & 0 0 & 1end{pmatrix} quad I_3=begin{pmatrix} 1 & 0 & 0 0 & 1 & 0 � & 0 & 1 end{pmatrix} quad I_n=(delta_{i,j})_{1le ile n,1le jle n}$

où $δ i, j$ désigne le symbole de Kronecker.

Sous réserve de compatibilité des tailles, les matrices I_n sont neutres à droite et à gauche pour la multiplication.

$forall Min M_{m,n}(A), I_m,M=M,I_n =M$

Soit M une matrice de dimension (m,n). On dit que M est inversible à droite (respectivement à gauche) si et seulement s'il existe une matrice N de taille (n,m) telle que $displaystyle MN = I_m$ (respectivement $displaystyle NM = I_n$ ). Pour une matrice carrée, à coefficients dans un anneau commutatif, être inversible à droite et à gauche sont deux propriétés équivalentes. Une matrice les vérifiant sera dite inversible, sans plus de précision. Le déterminant est une fonction importante sur les matrices carrées, qui permet notamment de tester leur inversibilité. Le sous-ensemble de $M n (A)$ constitué des matrices inversibles possède une structure de groupe pour le produit matriciel, est appelé groupe linéaire et noté $displaystyle GL_n(A)$ .

Algèbre des matrices carrées

Lorsque l'anneau $A$ est commutatif, l'ensemble des matrices carrées $M n (A)$ est donc muni d'une structure d'algèbre associative et unitaire avec l'addition matricielle, le produit par un scalaire et le produit matriciel.

On appelle matrice scalaire une matrice de la forme $a I n$ où $a$ est un élement de l'anneau $K$ .

$aI_n=begin{pmatrix} a & 0 & dots & 0 0 & a & dots & 0 vdots &vdots&ddots& vdots 0 & 0 &dots & a end{pmatrix}$

Ces matrices s'appellent matrices scalaires car elles se comportent comme des scalaires, vis-à-vis de la multiplication :

$forall ain A, forall Min M_n(A), (aI_n)M = acdot M$

Lorsque $A$ est commutatif, ou à défaut, losque $a$ est central dans $A$ , c'est-à-dire lorsque $a$ commute avec tous les éléments de $A$ , on a

$forall ain A, forall Min M_n(A), (aI_n)M = M(aI_n) = acdot M$

Réciproquement, toute matrice $N$ de $M n (A)$ telle que $forall Min M_n(A), MN = NM$ est une matrice scalaire $a I n$ où $a$ est central dans $M$ . Ceci se démontre en prenant pour M les matrices de la base canonique.

Une matrice de la forme :

$begin{pmatrix} a_1 & 0 & dots & 0 0 & a_2 & dots & 0 vdots &vdots&ddots& vdots 0 & 0&dots & a_n end{pmatrix}$

sera dite matrice diagonale.

Outre le déterminant, une autre fonction à noter est la trace. Toutes deux apparaissent dans un objet plus général, le polynôme caractéristique, qui à son tour permet d'obtenir certaines caractérisations des matrices diagonalisables (c'est-à-dire semblable — voir plus bas — à une matrice diagonale), ou de la trigonalisation.

EXERCICES

UNE Série d'exercices sur

http://www.sharo.fr/GN/Maths/Kholles/Exo/Calcul%20matriciel.pdf